Question

When Mason left his house in the morning, his cell phone battery was partially charged. Let BB represent the charge remaining in Mason's battery, as a percentage, tt hours since Mason left his house. The table below has select values showing the linear relationship between tt and B.B. Determine the charge of the battery when Mason left his house.

Answer 1

First, we will find the equation of the relationship between t and B.

A linear equation is of the form:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

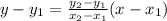
Where

(x1, y1) is a point the line goes through and (x2, y2) is another point the line goes through

Note: the independent variable here is t and the dependent is B. We will find the equation in the regular x and y variable, then change to t and B.

Let's take two points from the table:

`\begin{gathered} (x_1,y_1)=(1,42) \\ \text{and} \\ (x_2,y_2)=(5,18) \end{gathered}`

Now, we will substitute the points into the line equation and figure out the answer:

`\begin{gathered} y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1) \\ y-42=(18-42)/(5-1)(x-1) \\ y-42=(-24)/(4)(x-1) \\ y-42=-6(x-1) \\ y-42=-6x+6 \\ y=-6x+6+42 \\ y=-6x+48 \end{gathered}`

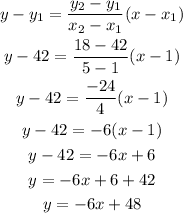
In terms of "t" and "B", we can write the equation as:

`B=-6t+48`

----------------------------------------------------------------------------------------------------------------

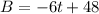
Now,

Plugging in t = 3 into the equation will give us the charge amount (B) after 3 hours:

`\begin{gathered} B=-6t+48 \\ B=-6(3)+48 \\ B=-18+48 \\ B=30 \end{gathered}`

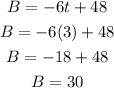
Thus, Melanie's phone had 30% battery charge after 3 hours she left home.