Given
height of the spray of water is given by
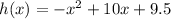
where , x is the number of feet away from the sprinkler head the spray is
Find
The irrigation system is positioned ----- feet above the ground to start.
The spray reaches a height of------- feet at horizontal distance of
feet away from the sprinkler head.
The spray reaches all the way to the ground at about ------ feet away.
Step-by-step explanation
to find the height above the ground to start,
we have to put x = 0
so , h(x) = 9.5
hence , the irrigation system is positioned 9.5 feet above the ground to start.
the axis of symmetry of quadratic is x = -b/2a
so ,for given quadratic ,

so , the maximum height is

hence , the spray reaches a height of 34.5 feet at horizontal distance of feet away from the sprinkler head.
the maximum distance will be

hence , the spray reaches all the way to the ground at about 10.9
feet away.
Final Answer
Hence , The irrigation system is positioned 9.5 feet above the ground to start.
The spray reaches a height of 34.5 feet at horizontal distance of
feet away from the sprinkler head.
The spray reaches all the way to the ground at about 10.9 feet away.