Question

The length of a rectangle is 4 inches longer than it is wide. If the area is 192 square inches, what are the dimensions of the rectangle?

Answer 1

Lets draw a picture of our problem:

where x denotes the wide of the rectangle.

Since the area of a rectangle is wide times length, we have that

`A=x(x+4)`

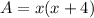
since A=192 square inches, we get

`\begin{gathered} 192=x(x+4) \\ or\text{ equivalently,} \\ x(x+4)-192=0 \end{gathered}`

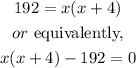
By distributing the variable x into the parenthesis, we have the following quadratic equation:

`x^2+4x-192=0`

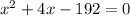
which we can solve it by applying the quadratic formula:

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{where},\text{ in our case,} \\ a=1 \\ b=4 \\ c=-192 \end{gathered}`

then, by substituting these values, we have

`x=\frac{-4\pm\sqrt[]{4^2-4(1)(-192)}}{2}`

which gives

`\begin{gathered} x=\frac{-4\pm\sqrt[]{16+768}}{2} \\ x=\frac{-4\pm\sqrt[]{784}}{2} \\ x=(-4\pm28)/(2) \end{gathered}`

so, the two solutions are:

`\begin{gathered} x_1=(-4+28)/(2)=(24)/(2)=12 \\ \text{and} \\ x_2=(-4-28)/(2)=(-32)/(2)=-16 \end{gathered}`

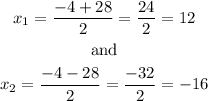
But a negative solution is not allowed because the dimensions are always positive numbers. Then, the searched variable x is 12. Then, the wide and length are, respectively,

`\begin{gathered} \text{ wide=x=12 inches} \\ \text{ length=x+4=12+4=16 inches} \end{gathered}`

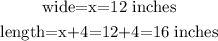
that is, the dimension of the rectangle are: wide is 12 inches and length is 16 inches.