Hello there. To solve this question, we have to remember some properties about exponential growth functions.
Given that the bacteria growing on the water's surface in a non-operational swimming pool from September 20 covers it entirely on September 28, we want to determine when will a quarter of the water's surface be covered.
For this, set the following function that gives you the water surface area covered by the bacteria:
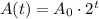
Whereas A0 is the initial area that, for calculation purposes, we consider it as the unit of area, hence A0 = 1 m².
And we know the total area of the pool is given by
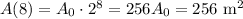
Now, we need to determine when a quarter of the pool will be covered in bacteria.
In this case, we want that
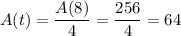
In this case, we get that
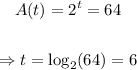
Hence we add it to the initial time observation in days:

The answer to this question is:
The water's surface will be covered a quarter of the way on September 26