In this case, we'll have to carry out several steps to find the solution.
Step 01:
Data:
distance = s
time = t
Step 02:
directly proportional:
s = kt²
k:
s = 16 ft
t = 1 s
16 ft = k * (1 s)²
16 ft = k * 1 s²
16 ft / s² = k
distance, t = 4 s:
s = 16 ft / s² * (4 s)² = 16 ft / s² * 16 s² = 256 ft
time, s = 144 ft:
144 ft = 16 ft / s² * t²
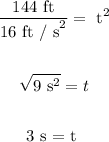
The answer is:
distance, t = 4 s:
s = 256 ft
time, s = 144 ft:
t = 3 s