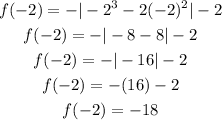1 Answer

Brady Dowling · Answer 1 · 2023-05-14T12:40:27+0000

Part 1

we have the equation

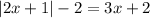
$\mleft|2x+1\mright|-2=3x+2$

Solve for x

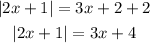
$\begin{gathered} |2x+1|=3x+2+2 \\ |2x+1|=3x+4 \end{gathered}$

REmember that the absolute value function has two solutions

First solution (case positive)

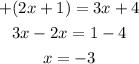
$\begin{gathered} +(2x+1)=3x+4 \\ 3x-2x=1-4 \\ x=-3 \end{gathered}$

Second solution (negative case)

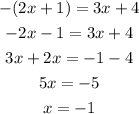
$\begin{gathered} -(2x+1)=3x+4 \\ -2x-1=3x+4 \\ 3x+2x=-1-4 \\ 5x=-5 \\ x=-1 \end{gathered}$

therefore

the solutions are x=-3 and x=-1

Part 2

we have the function

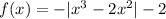
$f(x)=-\mleft|x^3-2x^2\mright|-2$

Remember that

f(-2) is the value of f(x) when the value of x=-2

substitute the value of x in the expression above

$\begin{gathered} f(-2)=-|-2^3-2(-2)^2|-2 \\ f(-2)=-|-8-8|-2 \\ f(-2)=-|-16|-2 \\ f(-2)=-(16)-2 \\ f(-2)=-18 \end{gathered}$

Please log in or register to add a comment.