Given
A ladder leans against a building, making a 46 degree, angle of elevation with the ground.
The top of the ladder reaches a point on the building that is 21 feet above the ground.
To find: The distance, x between the base of the building and the base of the ladder.
Step-by-step explanation:
It is given that,
The height of the building is 21 feet.
The angle of elevation is 46 degrees.
Therefore,
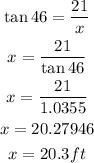
Hence, the value of x is 20.3ft.