B)272
Step-by-step explanation
An arithmetic sequence is defined as a series of numbers, in which each term (number) is obtained by adding a fixed number to its preceding term.
![Sum=(n)/(2)\mleft[2a+(n-1)d\mright],](https://img.qammunity.org/2023/formulas/mathematics/college/oc9gbgonr8d8e3roui4xc1pol5rauc6xdg.png)
where 'a' is the first term, 'd' is the common difference between two numbers, and 'n' is the number of terms.so
Step 1
Let
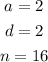
replace,
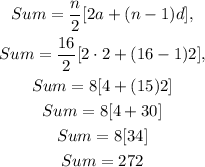
therefore, the answer is
B)272
I hope this helps you