Question

Solve 2 log 5 + log; x = logz 100.

Answer 1

The given expression is

`2\log _75+\log _7x=\log _7100`

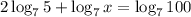
First, we have to use the power property of logarithms, which states

`a\log x=\log x^a`

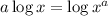
So, we have

`\log _75^2+\log _7x=\log _7100`

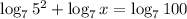
Now, we use the product property of logarithm, which states

`\log a+\log b=\log a\cdot b`

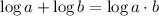
Then, we have

`\log _75^2\cdot x=\log _7100`

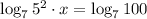
We can eliminate logarithms

`5^2\cdot x=100`

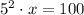
Now, we solve for x

`\begin{gathered} 25x=100 \\ x=(100)/(25)=4 \end{gathered}`

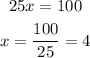
Therefore, the right answer is 4.