Answer: Provided the two functions, f(x) and g(x) we have to answer a to e parts:
(a) Graph of the region bounded by f and g and their points of intersection:
(b) Area of the region between the functions can be calculated by setting up an integral equation and then solving it, the integral is as follows:
![\begin{gathered} \text{ Area = Area line - Area curve} \\ \\ \\ A=A_l-A_c \\ \\ \\ A=\int_(-1)^3g(y)dy-\int_(-1)^3f(y)dy \\ \\ \\ A=\int_(-1)^36dy-\int_(-1)^(-3)[(y-1)^2+2]dy=\int_(-1)^3[6-(y-1)^2-2[dy \\ \\ \\ A=\int_(-1)^3[6-(y-1)^2-2]dy\rightarrow(1) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7laoynllcx8ap5wtvd8rv9n01web6ircbo.png)
The area is the value of the integral (1). Its value is as follows:
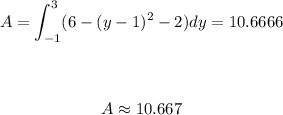
(c) Revolving the area between the functions around the y = -1.
When we include the line, the new graph looks as follows.
The new integral formulation, which would be used to calculate the volume of the new solid is as follows:
![V=\int_2^6\pi[√(x-2)+2]^2dx-\int_2^6\pi[-√(x-2)+2]^2dx\rightarrow(2)](https://img.qammunity.org/2023/formulas/mathematics/college/71q86ohzgml2oh5w8c06gzyd7tefv7cv7y.png)
The integral (2) represents the following:
Which is just the original f(y) shifted along the y-axis by 1 unit, the value of the integral (2) is as follows:
![\begin{gathered} V=\int_2^6\pi[√(x-2)+2]^2dx-\int_2^6\pi[-√(x-2)+2]^2dx \\ \\ \\ \\ V=\pi\int_2^6([√(x-2)+2]^2-[-√(x-2)+2]^2)dx=(32)/(3)\pi \\ \\ \\ \\ V=(32)/(3)\pi \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ydhpzr3ygav65ngk7j92e4dag1xgm4iucc.png)