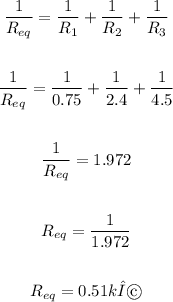Answer:
a) The equivalent resistance in series = 7.65 kΩ
b) The equivalent resistance in parallel = 0.51 kΩ
Step-by-step explanation:
The resistances of the given resistors are:
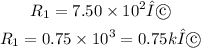
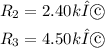
The equivalent resistance in series:
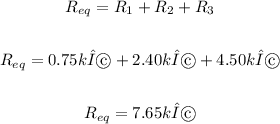
b) The equivalent resistance in parallel