Question

1. ENERGY In 2015 , it is estimated that the United States used about 51,000 quadrillion thermal units. If U.S. energy consumption increases at a rate of about $0.6 \%$ annually, what amount of energy will the United States use in 2020 ?a) $52,448.47 Q$ b) $52,548.47 Q$ c) 52,648.47 Q d) 54,748.47 Q2. BIOLOGY The number of rabbits in a field showed an increase of 15% each month over the last year. If there were 12 rabbits at this time last year, how many rabbits are in the field now?a) 34 b) 44 c) 54 d) 64

Answer 1

(B)52,548.47 Quadrillion Units.

(D)64 rabbits

Step-by-step explanation:

Number 1

Energy consumption in 2015 = 51,000 Quadrillion Units

Rate of Increase per year = 0.6%

2020 - 2015 = 5years

We can model this problem using an exponential growth function.

`\begin{gathered} E(t)=E_0(1+r)^t \\ \text{Where: }E(t)=\text{Energy consumed in t years after 2015} \\ E_0=\text{Energy consumed in 2015} \\ r=\text{Growth rate} \end{gathered}`

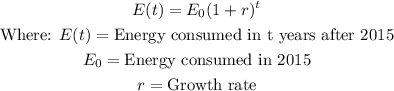
Substituting the given values, we have:

`\begin{gathered} E(t)=51000(1+(0.6)/(100))^5 \\ =51000(1+0.006)^5 \\ =51000(1.006)^5 \\ =52548.47 \end{gathered}`

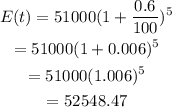
The energy consumed in 2020 is 52,548.47 Quadrillion Units.

Number 2

Number of rabbits last year = 12

Rate of Increase per month = 15%

Time = 12 months

We can model this problem using an exponential growth function.

`\begin{gathered} P(t)=P_0(1+r)^t \\ \text{Where: }P(t)=\text{Number of rabbits after t months} \\ P_0=\text{Initial population of rabbits} \\ r=\text{Growth rate} \end{gathered}`

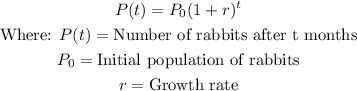
Substituting the given values, we have:

`\begin{gathered} P(t)=12(1+(15)/(100))^(12) \\ =12(1+0.15)^(12) \\ =12(1.15)^(12) \\ =64 \end{gathered}`

The number of rabbits in the field now is 64.