Question

Which of the following represents the critical points thatdefine the test intervals for the rational inequality *² +4×-21 <0?x-5

Answer 1

The Solution:

Given:

`(x^2+4x-21)/(x-5)\leq0`

Required:

Find the critical points of the given rational inequality.

Recall:

The critical values are simply the zeros of both the numerator and the denominator.

Thus, the critical points are:

`\begin{gathered} x-5=0 \\ x=5 \\ \\ solve\text{ the quadratic equation:} \\ x^2+4x-21=0 \\ x^2+7x-3x-21=0 \end{gathered}`
`\begin{gathered} x(x+7)-3(x+7)=0 \\ (x-3)(x+7)=0 \\ x-3=0 \\ x=3 \\ or \\ x+7=0 \\ x=-7 \\ \end{gathered}`

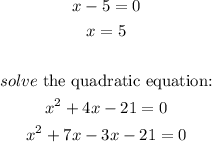
Thus, the critical points are:

`x=5,\text{ }x=3\text{ or }x=-7`

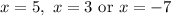
Therefore, the correct answer is [option C]