Two lines are perpendicular when the product between the slopes of the lines is equal to -1, then, if we have the following lines:
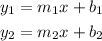
they will be perpendicular if,
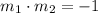
According to the exercise, the first line is:
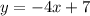
the slope for this line is -4.
Write the equation that makes two lines perpendicular,
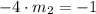
solve for m2,
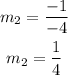
Answer:
The slope of the line perpendicular to y=-4x+7 is 1/4.