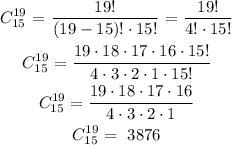Question

Someone help I think this is probability but I don’t know

Answer 1

1. 3391680

2. 3876

Step-by-step explanation

1. We want to find the value of:

`P^(12)_7`

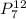
This is called "12 permutation 7"

Permutation function is defined as follows:

`P^n_r\text{ = }(n!)/((n-r)!)`

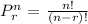
Therefore, we have that:

`\begin{gathered} P^(12)_7=\frac{12!}{(12\text{ - 7)}!}\text{ = }(12!)/(5!) \\ P^(12)_7=(12\cdot11\cdot10\cdot9\cdot8\cdot7\cdot6\cdot5!)/(5!) \\ P^(12)_7=\text{ 12 }\cdot11\cdot10\cdot9\cdot8\cdot7\cdot6 \\ P^(12)_7=3391680 \end{gathered}`

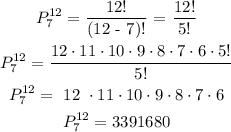
2. We want to find:

`C^(19)_(15)`

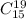
This is called "19 combination 15"

Combination function is defined as:

`C^n_r=\frac{n!}{(n-r)!\cdot r!_{}}`

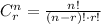
Therefore, we have that:

`\begin{gathered} C^(19)_(15)\text{ = }(19!)/((19-15)!\cdot15!)\text{ = }(19!)/(4!\cdot15!) \\ ^{}C^(19)_(15)=(19\cdot18\cdot17\cdot16\cdot15!)/(4\cdot3\cdot2\cdot1\cdot15!) \\ C^(19)_(15)=(19\cdot18\cdot17\cdot16)/(4\cdot3\cdot2\cdot1) \\ C^(19)_(15)=\text{ 3876} \end{gathered}`