Question

OCPS Dashboardirtual SchoolLessons Assessments ✔GradebookQuestion 5Mutiple Choice Worth 1 points)(08.05 MC)The following graph describes function 1, and the equation below it describes function 2. Determine which function has a greater maximum value, and provide the ordered pair.Function 1Function 1 has the larger maximum at (4, 1).05(10)-0.5Function 210x)=-x²+2x-15.Exam: 08.11 Segment Two Exam Part Two - Algebra 1 V23 (Email Tools -

Answer 1

Given:

Function 1 is given in the graph.

Function 2 is,

`f(x)=-x^2+2x-15`

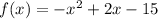
To find:

The function has a larger maximum value.

Step-by-step explanation:

From the graph,

We know that the maximum value of the function is the highest point of the function.

For the function 1, the maximum value is 1 at x = 4.

For the function 2,

Differentiating with respect to x, we get

`f^(\prime)(x)=-2x+2`

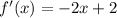
Equate it with zero, and we get

`\begin{gathered} -2x+2=0 \\ x=1 \end{gathered}`

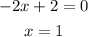
Substituting x = 1 in function 2.

`\begin{gathered} f(1)=-1^2+2(1)-15 \\ =-14 \end{gathered}`

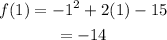
So, the maximum value is -14 at x = 1.

Then, comparing functions 1 and 2 we get,

Function 1 has the larger maximum value at (4, 1).

Final answer:

Function 1 has the larger maximum value at (4, 1).