We will assign a variable to the total capacity of Christine's penny bank to hold pennies as:
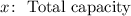
The bank was initally full to some extent expressed as a fraction of the total capacity of the penny bank as follows:
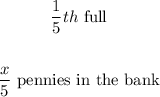
She then adds a certain number of pennies in the bank as follows:

The total capacity of the bank utilized/filled with pennies can be expressed as a sum of inital capacity and the number of pennies Christine added as follows:
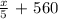
Christine find that after adding 560 pennies to the bank it was filled to a new fraction of the total capacity as follows:
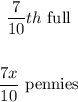
We can equate the expression for number of pennies in the bank to the fraction above as follows:
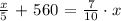
We have an equation with one variable ( x ). We can solve the above equation by algebraic manipulation as follows:
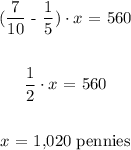
Hence, the total number of pennies that Christine's bank can withold is:
