Answer:
• Potential Roots are: 1, -1, 1/2, -1/2, 2,-2,4, and -4.
,
• Actual roots: -1 and -2.
,
• Code piece: H.
Explanation:
Given the polynomial:
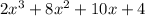
Applying the rational Toot theorem:
The constant = 4
• The factors of the constant, p = ±1,±2, and ±4
The leading coefficient = 2
• The factors of the leading coefficient, q = ±1 and ±2.
The potential roots are obtained below:
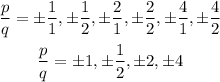
Potential Roots are: 1, -1, 1/2, -1/2, 2,-2,4, and -4.
Next, find the actual roots by substituting each of the potential roots for x:
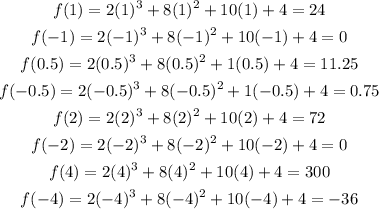
From the calculations above, the actual roots are -1 and -2.
Thus, the actual roots are:
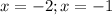
The code piece is H.