Given:
Area of the rectangle is 50 sq. m.
The length of the rectangle is 5 m less than three times the width.
That is,
l=3w-5
To find the dimensions:
The formula for the area of the rectangle is , A=lw
Therefore,

Since, width can not be negative.
So, -10/3 can be neglected.
Hence, w=5
So, the length is,
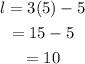
Hence, the dimensions are, l=10 m and w=5 m.