Question

Use the diagram as a reference to answer the question below

Answer 1

Let us draw out the triangle below:

Given that

`\arctan \frac{\sqrt[]{3}}{3}=\beta`

Using the trigonometric identity for tan 30, where

`\tan 30=\frac{\sqrt[]{3}}{3}`

Therefore,

`\beta=30\degree`

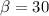
The sum of angles in a triangle is 180°.

Therefore,

`\begin{gathered} \alpha+\beta+90=180\degree \\ \therefore \\ \alpha+30+90=180 \\ \alpha=180-90-30 \\ \alpha=60\degree \end{gathered}`

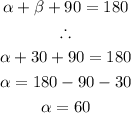
To get the sides of the triangle, let us apply the Trigonometric ratios:

Using the Sine Trig. ratio,