Question

Question 3:A store did $31,000 in sales in 2014, and $49,000 in 2018.(a) Assuming the store's sales are growing linearly, find the growth rate d.(b) Write a linear model of the form Pt=P0+dt to describe this store's sales from 2014 onward.Pt= (c) Predict the store's sales in 2025.$ (d) When do you expect the store's sales to exceed $105,000? Give your answer as a calendar year (ex: 2020).During the year

Answer 1

(a) In order to find the growth rate d, use the following formula:

`d=\frac{P_2-P_1_{}}{t_2-t_1_{}}`

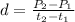
where

P2 = 49000

P1 = 31000

t2 = 2018

t1 = 2014

Replace the previous values of the patameters into the formula for d:

`d=(49000-31000)/(2018-2014)=(18000)/(4)=4500`

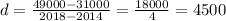
Hence, the growth rate is $4500 per year.

(b) In order to write the store's sales as a linear model, use the following general equation for a line:

`P-P_1=d(t-t_1)`

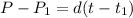
Replace the values of P1 and t1 and solve for P, as follow:

`\begin{gathered} P-31000=4500(t-0) \\ P=4500t+31000 \end{gathered}`

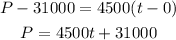
In this case we used t = 0 because we need a model to determine the store's sale from 2014 onward, which is equivalent that year 2014 is t = 0.

Hence, the linear model is

P(t) = 31000+4500t

(c) For 2025, t = 2025 - 2014 = 11, then, you have:

`P(11)=31000+4500(11)=31000+49500=80500`

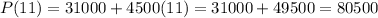
Hence, the stores's sale for 2025 will be $80500

(d) To determine the year when store's sales will exceed $105,000, replace P(t) = 105000 into the expression for P(t) and solve for t:

`\begin{gathered} 105000=31000+4500t \\ 105000-31000=4500t \\ 74000=4500t \\ (74000)/(4500)=t \\ t\approx16.4 \end{gathered}`

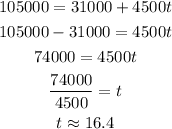
Consider that the counting is from 2014, then:

2014 + 16.4 = 2020.4

Which is equivalent to the year 2020.

Then, during the year 2020, we expect the store's sales exceed $105,000