We are given the following function:

Part A. We are asked to determine the following:

This means the composition of the function "f" and "g". To do that we will use the following equivalence:
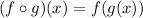
This means that we will substitute the value of "x" from function "f" by the function "g", like this:
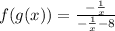
Now, we simplify the fraction:
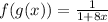
To determine the domain we must set the denominator to zero to determine the values of "x" for which the composition of the functions is undetermined:
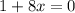
Now, we solve for "x". First, we subtract 1 from both sides:
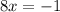
Now, we divide both sides by 8:
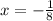
Therefore, the composition is undetermined at the point "x = -1/8". Therefore, the domain is:
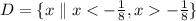
Part B. we are asked to determine the following:
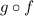
This is equivalent to:
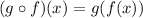
This means that we will substitute the value of "x" from function "g" for the value of function "f", like this:

Now, we simplify the expression:
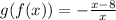
To determine the domain we set the denominator to zero:

Therefore, the function is undetermined at "x = 0". This means that the domain is the values of "x" that do not include the value of "x = 0":

Part C. We are asked to determine:
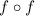
This is equivalent to:
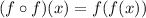
Now, we substitute the value of "x":
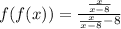
Now, we multiply the numerator and denominator by "x - 8":
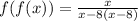
Applying the distributive property and adding like terms we get:
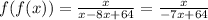
Now, we set the denominator to zero to determine the domain:
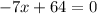
Now, we subtract 64 from both sides:
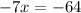
Now, we divide both sides by -7:
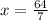
Therefore, the domain does not include the value of "x = 64/7". Therefore, the domain is:
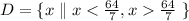
Part D. We are asked to determine:

Substituting the value of "g(x)" in "g(x)" we get:
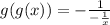
Simplifying we get:
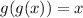
To determine the domain we need to have into account that the function is a polynomial and therefore, is not undetermined at any point. This means that the domain is all the real numbers.