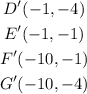Question

Write the coordinates of the vertices after a rotation 90° counterclockwise around the origin.-10 -8-6GD-4-21048642E-2-4-6-8-102468Ao10M

Answer 1

Given:

The coordinates of the vertices are,

`\begin{gathered} D(-4,1) \\ E(-1,1) \\ F(-1,10) \\ G(-4,10) \end{gathered}`

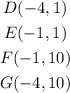
To find:

The coordinates of the vertices after rotating 90 degrees counter-clockwise direction.

Step-by-step explanation:

The transformation rule is,

`(x,y)\rightarrow(-y,x)`

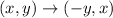
Applying the rule,

The coordinates of the vertices become,

`\begin{gathered} D^(\prime)(-1,-4) \\ E^(\prime)(-1,-1) \\ F^(\prime)(-10,-1) \\ G^(\prime)(-10,-4) \end{gathered}`

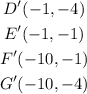
Final answer:

The coordinates of the vertices are,

`\begin{gathered} D^(\prime)(-1,-4) \\ E^(\prime)(-1,-1) \\ F^(\prime)(-10,-1) \\ G^(\prime)(-10,-4) \end{gathered}`