Maximum (-1,5)
Step-by-step explanation:
The vertex of an up - down facing parabola of the form

is
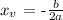
. Quadratic form of the function
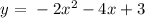
The parameters become
a = -2
b = -4
c = 3
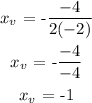
To find y(v) simply put x(v) in the function
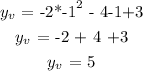

NB:
If a < 0, then the vertex is a maximum value (Which is the case here since -2 < 0)
If a > 0, then the vertex is a minimum value