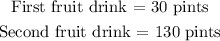Question

Solve this percent mixture problem using a system of linear equationsThe royal fruit company produces two types of fruit drinks. The first type is 20% pure fruit juice, and the second type is 100% pure fruit juice. The company is attempting to produce a fruit drink that contains 85% pure fruit juice. How many pints of each of the two existing types of drink must be used to make 160 pints of a mixture that is 85% pure fruit juice? First Fruit Drink= Pints Second Fruit Drink= Pints

Answer 1

Let x and y represent the amount of the first and second type of fruit drinks (respectively) that are used to create the fruit drink that contains 85% fruit juice.

The total volume of the mixture is x+y and it must be equal to 160:

`x+y=160`

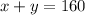
Since the first mixture contains 20% fruit juice, only 0.2x of the volume x is pure fuit juice. The total amount of fruit juice in the mixture will be 0.2x plus y, and must be equal to 85% of 160:

`0.2x+y=0.85\cdot160`

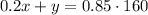
We got a system with two variables and two equations. Solve the system of equations using the elimination method:

`\begin{gathered} x+y=160 \\ 0.2x+y=0.85\cdot160 \\ \Rightarrow x-0.2x+y-y=160-0.85\cdot160 \\ \Rightarrow0.8x=160-136 \\ \Rightarrow0.8x=24 \\ \Rightarrow x=(24)/(0.8) \\ \therefore x=30 \end{gathered}`

Replace x=30 into the first equation to find the value of y:

`\begin{gathered} x+y=160 \\ \Rightarrow30+y=160 \\ \Rightarrow y=160-130 \\ \Rightarrow y=130 \end{gathered}`

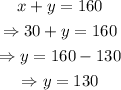
Then, 30 pints of the 20% pure fruit juice and 130 pints of the 100% pure fruit juice are needed to produce 160 pints of the 85% pure fruit juice mixture.

Therefore, the answer is:

`\begin{gathered} \text{First fruit drink = 30 pints} \\ \text{Second fruit drink = 130 pints} \end{gathered}`