Question

Solve 12 and label part A and B, make sure you do both a and b

Answer 1

(a)

`g^(\prime)(s)=2s-2`

(b) The answer in part (b) agrees with that of part (a)

Step-by-step explanation:

Given:

`g(s)=(4s^3-8s^2+4s)/(4s)`

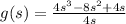
a) We'll go ahead and determine the derivative of g(s) as seen below;

`\begin{gathered} Let\text{ }u=4s^3-8s^2+4s \\ u^(\prime)(s)=12s^2-16s+4 \\ Let\text{ }v=4s \\ v^(\prime)(s)=4 \end{gathered}`

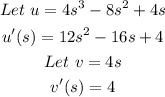
Let's go ahead and substitute the above values into the below Quotient Rule formula and simplify;

`\begin{gathered} g^(\prime)(s)=(vu^(\prime)(s)-uv^(\prime)(s))/(u^2) \\ \\ =(4s(12s^2-16s+4)-(4s^3-8s^2+4s)(4))/((4s)^2) \\ \\ =(48s^3-64s^2+16s-16s^3+32s^2-16s)/(16s^2) \\ \\ =(32s^3-32s^2)/(16s^2) \\ \\ =(32s^3)/(16s^2)-(32s^2)/(16s^2) \\ \\ =2s-2 \\ \\ \therefore g^(\prime)(s)=2s-2 \end{gathered}`

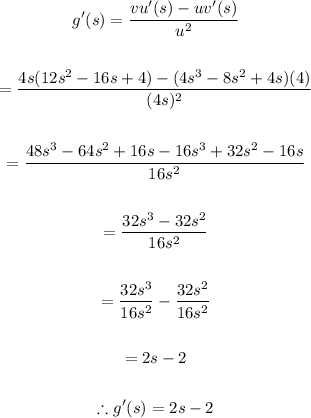
b) Let's go ahead and simplify g(s) as seen below;

`\begin{gathered} g(s)=(4s^(3)-8s^(2)+4s)/(4s) \\ \\ =(4s^3)/(4s)-(8s^2)/(4s)+(4s)/(4s) \\ \\ \therefore g(s)=s^2-2s+1 \\ \\ g^(\prime)(s)=2s-2+0 \\ \\ \therefore g^(\prime)(s)=2s-2 \end{gathered}`

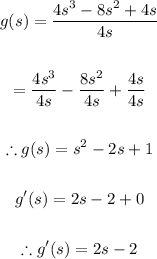
We can see from the above that the answer in part (b) agrees with that of part (a)