Question

Can you please help me with 52(For the following exercise, given the graph of the hyperbola, find its equation)

Answer 1

The equation for a hyperbola is different if it is horizontal or vertical.

In this case, we have a horizontal hyperbola, so the equation is:

`((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1^{}_{}`

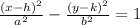
Now, we just need to identify h, k, a and b from the graph.

The values of h and k are the coordinates of the center of the hyperbola, (h, k).

The center is shown to be (1, 1), so:

`\begin{gathered} h=1 \\ k=1 \end{gathered}`

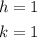
The value of a is the distance from the center to the vertices. Since its is a horizontal hyperbola, the distance is horizontal distance and can be calculated just using the x values.

We can use either vertices. Using the right one, 1 + √2, we have:

`\begin{gathered} a=|1+\sqrt[]{2}-1| \\ a=|\sqrt[]{2}| \\ a=\sqrt[]{2} \end{gathered}`

Now, to find be, we will need to use the following:

`a^2+b^2=c^2`

Where c is the distance from the center to either foci.

Let's use the right focus. Since again this is a horizontal distance, we can use only the x coordinate of the focus, 1 + √5.

So:

`\begin{gathered} c=|1+\sqrt[]{5}-1| \\ c=|\sqrt[]{5}| \\ c=\sqrt[]{5} \end{gathered}`

Now, we can find b, but since we will use b², we can find it instead, we don't need to go as further as finding b:

`\begin{gathered} a^2+b^2=c^2 \\ b^2=c^2-a^2 \\ b^2=(\sqrt[]{5})^2-(\sqrt[]{2})^2 \\ b^2=5-2 \\ b^2=3 \end{gathered}`

Now, we have all we need:

`\begin{gathered} a^2=(\sqrt[]{2})^2=2 \\ b^2=3 \\ h=1 \\ k=1 \end{gathered}`

So, the equation is:

`((x-1)^2)/(2)-((y-1)^2)/(3)=1`