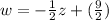SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given details
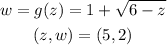
STEP 2: Explain Tangent line
Tangent Lines:
The tangent line to a function f(x) is a line that touches the graph of the function at one specific point of tangency where it has the same slope as the function at that point.
If x = a is the point of tangency, the tangent line can be written in slope-intercept form as:
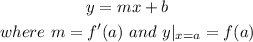
STEP 3: Find the tangent
We can first determine the slope of the tangent line by differentiating the function. Writing the function as:
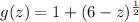
We find the derivative using the chain rule:
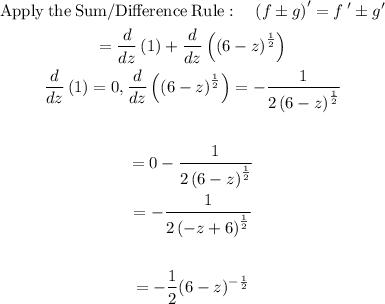
At the point of tangency, the slope is
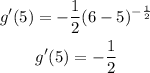
We can begin to write the equation of the tangent line in slope-intercept form
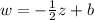
Substituting both coordinates of the point of tangency allows us to solve for the intercept:
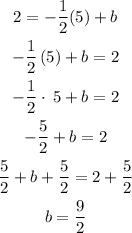
The complete equation of the tangent line at (5,2) is then