Question

This is 8th grade math, Would you please clear up how to do it on my own?

Answer 1

From the graph, we can recognize two functions:

From the graph, we have that the blue graph is the absolute value function:

`y(x)=|x+3|`

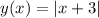
We can take the coordinates of the points:

(-7, 3) and (-3, 0)

(5, 6) and (-3, 0)

The slope for the first case is -3/4 and the second case is 3/4. Then the lines are from this function.

In the second case, we have a parabola if we connect the points from the graph. We can see from the coordinates that the vertex is in x = 5, and y = -6. And the graph can be described by the function:

`y(x)=(x-5)^2-6`

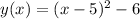
Since the x is shifted five units to the right (x-axis) and 6 units below in the y-axis.

Here we have two functions. If we have these two functions at the same time, we will end with two ranges, and to be a function one needs the function will have only one range. Therefore, this graph does not represent a function (in fact it represents two functions).