Step 1
State the formula for Future value compounded monthly.
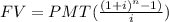
where;
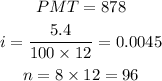
Step 2
Find the future value

Find how much of the future value is interest
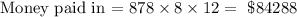

Hence, the answers are;
How much is in the account after 8 years = $105134.28 to 2 decimal places
How much of this is interest = $20846.28 to 2 decimal places