Question

Find the gravitational force between Saturn (5.68 x 10^26kg ) and the sun (1.99 x 10^30 kg). Saturn orbits at a distance of 1,404,219,991,220 m.

Answer 1

`3.826\cdot10^(22)N`

Step-by-step explanation

To find the gravitational force between them, apply the formula for gravitational force:

`F=(GmM)/(r^2)`

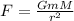
where G = gravitational constant = 6.6743 * 10^(-11) Nm²/kg²

m = mass of Saturn

M = mass of the sun

r = distance between them (radius of Saturn's orbit)

Therefore, the gravitational force between them is:

`\begin{gathered} F=(6.6743\cdot10^(-11)\cdot5.68\cdot10^(26)\cdot1.99\cdot10^(30))/((1,404,219,991,220)^2) \\ F=(75.4409\cdot10^(-11+26+30))/(1.9718\cdot10^(24))=(7.54409\cdot10^(46))/(1.9718\cdot10^(24)) \\ F=3.826\cdot10^(22)N \end{gathered}`