Question

Find the missing probability.P(A∩B)=3/100,P(B|A)=3/20,P(A)=?A. 3/10B. 13/40C. 1/5D. 39/400

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given probabilities

`\begin{gathered} p(A\cap B)=(3)/(100) \\ p(B|A)=(3)/(20) \\ p(A)=? \end{gathered}`

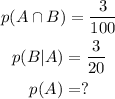
STEP 2: Write the formula for conditional probability

`p(B|A)=(p(A\cap B))/(p(A))`

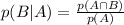
STEP 3: Get the value of the requried probability

By Substitution,

`\begin{gathered} (3)/(20)=((3)/(100))/(p(A)) \\ \\ (3)/(20)=(3)/(100* p(A)) \\ Cross\text{ Multiply} \\ 3(100p(A))=3*20 \\ 300* p(A)=60 \\ p(A)=(60)/(300)=(1)/(5) \end{gathered}`

Hencce, p(A) = 1/5