Question

Question 1 the sum of three consecutive integers is 126. the value of the GREATEST number is ____

Answer 1

43

Explanation

Step 1

let x represents the first number

first number=X

as the number are consecutives, the second number would be

`\begin{gathered} \text{second number= first number +1} \\ \text{second number=x}+1 \end{gathered}`

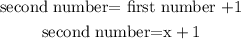
and the third number would be

`\begin{gathered} \text{third number= second number +1} \\ \text{third number=(x}+1)+1 \\ \text{third number=x}+2 \end{gathered}`

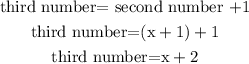
Now, we are told the sum of the three consecutive numbers is 126,so

`\text{first number+second number+thir number=126}`

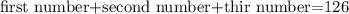
replace

`x+(x+1)+(x+2)=126\rightarrow equation\text{ (1)}`

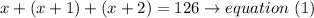
Step 2

solve the equation

`\begin{gathered} x+(x+1)+(x+2)=126\rightarrow equation\text{ (1)} \\ x+x+1+x+2=126\rightarrow equation\text{ (1)} \\ \text{add like terms} \\ 3x+3=126 \\ \text{subtract 3 in both sides} \\ 3x+3-3=126-3 \\ 3x=123 \\ \text{divide both sides by 3} \\ (3x)/(3)=(123)/(3) \\ x=41 \end{gathered}`

Step 3

finally, replace the x value to find the numbers

`\begin{gathered} \text{first number= x} \\ \text{first number=}41 \\ \text{second number = x+1}=41+1 \\ \text{second number = }42 \\ \text{third number=x+2=41+2} \\ \text{third number=}43 \end{gathered}`

theferore, the greatest number is 43

I hope this helps you