SOLUTION
The question provides us with a cylinder with a radius of 2 units and a height of 8 units.
We have been given a set of parameters to calculate and we are told to use pi = 3.14.
In order to solve for each parameter, we shall provide the formula for getting the parameter, when needed.
Circumference of the base:
The base of a cylinder is a circle with a radius of 2 units.
The formula for calculating the circumference of a circle is:
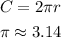
Thus, let us calculate the circumference:
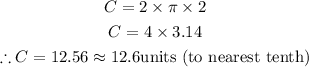
Area of the base:
Since the base of the cylinder is still the same circle, the formula for calculating the area of a circle is:
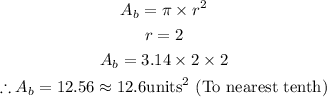
Height:
The height of the cylinder has already been given to be 8 units from the question as shown below:
Lateral Area:
The lateral area of the cylinder is the area of the sides of the cylinder without giving any consideration to the base of the cylinder.
The formula for calculating the Lateral area is:

With this formula given, let us proceed to find this area
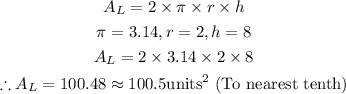
Finally,
Surface Area:
This is the sum of all the areas of all the surfaces on the cylinder. It is simply the addition of the base areas (Both top and bottom circles of the cylinder) with the lateral area.
Thus, we have:
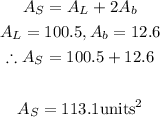
Let us recap our answers below:
Circumference of Base = 12.6 square units
Area of Base = 12.6 square unites
Height = 8 units
Lateral Area = 100.5 square units
Surface Area = 1`13.1 square units