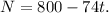Question

When a new charter school opened in 2000, there were 800 students enrolled. Write an equation representing the number, N, of students attending this charter school t years after 2000, assuming that the student population:

Answer 1

To solve these problems, we will use the following formulas:

1.- For linear increase or decrease:

`y=b\pm ax.`

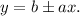
2.-For a percentage of increase or decrease:

`y=(1\pm r)^x.`

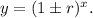
3.- A constant function is represented by:

`\begin{gathered} y=k, \\ k\text{ is a constant.} \end{gathered}`

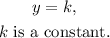
Answer:

a) Increases by 23 students per year:

`N=23t+800.`

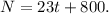
b) Decreases by 11% per year:

`N=800(1-0.11)^t=800(0.89)^t\text{.}`

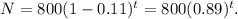
c) Increases by 15% per year:

`N=800(1+0.15)^t=800(1.15)^t.`

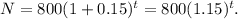
d) Remains constant:

`N=800.`

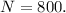
e) Decreases by 74 students per year:

`N=800-74t\text{.}`