Question

$9500 is invested, part of it at 12% and part of it at 7%. For a certain year, the total yield is $960.00. How much was invested at each rate?SIwas invested at 12%.

Answer 1

The total money was divided in two parts to be invested. Let's call the first part as 'x', and the other part 'y'. We know that the total amount sums up to $9500, then, we have the following equation:

`x+y=9500`

We also know that the first part is invested at 12% yearly, and the second one at 7% rate. The total yield is $960. Converting this into a mathematical equation, we have:

`0.12x+0.07y=960`

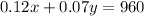
Now, we have a system with two equations and two variables.

`\begin{cases}x+y=9500 \\ 0.12x+0.07y=960\end{cases}`

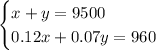
Rewriting the first equation to be x as a function of y, we have

`\begin{cases}x=9500-y \\ 0.12x+0.07y=960\end{cases}`

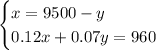
Now, making a substitution(the x in the first equation for the x in the second equation)

`\begin{gathered} 0.12(9500-y)+0.07y=960 \\ 1140-0.12y+0.07y=960 \\ 1140-960=0.05y \\ 180=0.05y \\ y=(180)/(0.05)=3600 \end{gathered}`

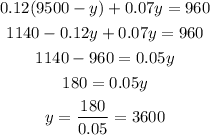
Now, using our y value in any of our previous equations we get the value for x.

`x=9500-3600=5900`

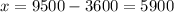
This means we invested $5900 at 12% and $3600 at 7%.