Question

JK is on the coordinate plane with J located at (7, -5) and Klocated at(-5,3). L is a point on JK that is 3 times closer to point than it is topoint K. What are the coordinates of point L?A. (-2, 1)B. (1, -1)C. (2, -2)D. (4, -3)

Answer 1

The points J is given as,

`J=(x_(1,)y_1)=(7,-5)\text{ }`

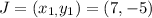
The point K is given as,

`K=(x_(2,)y_2)=(-5,3)`

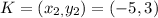
L is a point on JK that is 3 times closer to point J (assuming) than it is to point K.

Which means that the ratio is

`3\colon1`

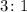
The coordinates of point L can be found by,

`(a\cdot x_1+b\cdot x_2)/(a+b),\text{ }(a\cdot y_1+b\cdot y_2)/(a+b)`

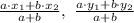
Where a:b = 3:1

So let us substitute the given coordinates into the above equation

`(3\cdot(7)+1\cdot(-5))/(3+1),\text{ }(3\cdot(-5)+1\cdot(3))/(3+1)`

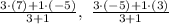
Simplify the equation,

`(21-5)/(4),\text{ }(-15+3)/(4)`
`(16)/(4),\text{ }(-12)/(4)`
`L=(4,-3)`

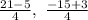
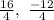
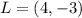
Therefore, the coordinates of point L are (4, -3)

The correct option is D.