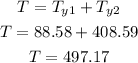Question

4. A 50.0-kg homogeneous beam supports a mass of 15.0 kilograms,as shown. The center of gravity of the beam is at the midpoint ofthe beam. Find the magnitude of the tension, T, in the rope.D. 0.01 10

Answer 1

First let's find the tension generated by the mass of 15 kg.

We can use the following formula to find this tension component:

`\begin{gathered} T_(y1)=m\cdot g\cdot\sin (\theta) \\ T_(y1)=15\cdot9.81\cdot\sin (37\degree) \\ T_(y1)=15\cdot9.81\cdot0.602 \\ T_(y1)=88.58\text{ N} \end{gathered}`

Now, to find the tension generated by the beam, first let's find the angle from the connection point of the rope with the wall and the center of gravity of the beam:

`\begin{gathered} \tan (37\degree)=(x)/(5) \\ 0.754=(x)/(5) \\ x=3.77 \\ \\ \tan (\theta)=(x)/(2.5) \\ \tan (\theta)=(3.77)/(2.5) \\ \text{tan(}\theta)=1.508 \\ \theta=56.45\degree \end{gathered}`

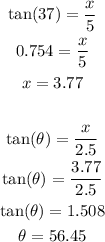
Now, let's use the same formula we used in the beggining:

`\begin{gathered} T_(y2)=m\cdot g\cdot\sin (\theta) \\ T_(y2)=50\cdot9.81\cdot\sin (56.45\degree) \\ T_(y2)=50\cdot9.81\cdot0.833 \\ T_(y2)=408.59 \end{gathered}`

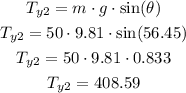
Adding both tensions, we have:

`\begin{gathered} T=T_(y1)+T_(y2) \\ T=88.58+408.59 \\ T=497.17 \end{gathered}`