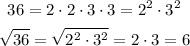In order to find if an integer is perfect, we need first to factor the number into prime factors.
For example, let's factor the number 16:
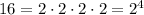
Since the exponent of all prime factors is even, that means the number has a square root that is an integer:
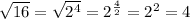
Let's use another example: number 36: