Question

Find the equation of line that passes though he point (6,5) and perpendicular to 3x-4y=8

Answer 1

3y + 4x = 39

Step-by-step explanation:

The formula for calculating the equation of a line in point-slope form is expressed as:

`y-y_0=m(x-x_0)`

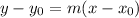
where;

m is the slope

(x0, y0) is the point on the line

Get the slope of the required line

Given the equation of the line 3x - 4y = 8

Rewrite in standard form

-4y = -3x + 8

y = -3x/-4 + -8/4

y = 3/4 x - 2

The slope of the given line is 3/4

If the equation of the required line is perpendicular to the given line, hence the slope of the required will be:

`\begin{gathered} M=(-1)/(((3)/(4))) \\ M=(-4)/(3) \end{gathered}`

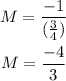
Get the equation of the required line:

`\begin{gathered} y-5=-(4)/(3)(x-6) \\ 3(y-5)=-4(x-6) \\ 3y-15=-4x+24 \\ 3y+4x=24+15 \\ 3y+4x=39 \end{gathered}`

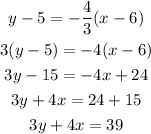
Hence the required equation of the line is 3y + 4x = 39