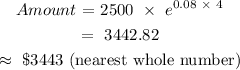Question

you have decided to invest $2500 at an 8% annual rate of interest how much will you have accumulated after 4 years if the interest is compounded continuously

Answer 1

For interest compounded continuously, the relationship between the future value(FV) and present value (PV) IS :

`FV\text{ = PV }*\text{ }e^{(i\text{ }*\text{ t)}}`

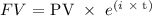
where:

i is the interest rate

t is the time in years

Using the given data:

PV = $ 2500

i = 8%

t = 4 years

The amount that would have been accumulated after 4 years:

`\begin{gathered} Amount\text{ = 2500 }*\text{ }e^{0.08\text{ }*\text{ 4}}^{} \\ =\text{ 3442.82} \\ \approx\text{ \$3443 (nearest whole number)} \end{gathered}`