Let x = the speed of the boat in still water while y = the rate/speed of the current in km/h.
Recall that:
upstream speed = speed of the boat in still water - speed of the current.
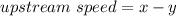
downstream speed = speed of the boat in still water + speed of the current.
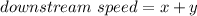
Let's calculate the upstream and the downstream speed of the motorboat based on the given distance and time traveled.
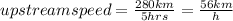
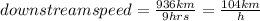
Hence, the upstream speed is 56 km/hour. The downstream speed is 104 km/h.
From the equation above, we can form the following equations:
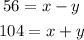
To solve for x and y, we can use the elimination method.
1. Eliminate the variable "y" by adding the two equations.
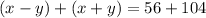
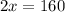
2. Divide both sides by 2.
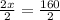
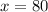
The value of x is 80.
3. Let's solve for "y" by replacing "x" with 80 in any of the two equations above.
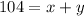
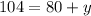

The value of y is 24.
Answer:
The rate of the boat in still water is 80 km per hour. The rate of the current is 24 km per hour.