Question

Each cable of a suspension bridge is suspended (in the shape of a parabola) between two towers (see figure).

Answer 1

Given:

There is a diagram given in the question

Required:

We need to find the equation of parabola and focus

Step-by-step explanation:

As we can see that vertex point of parabola is origin

`(0,0)=(h,k)`

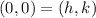
the general equation of parabola is

`y=a(x-h)^2+k`

now substitute the values

`y=ax^2`

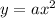
now by diagram there is a point

`(60,20)`

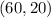
we use this point to find the a

Plug the point in equation

`\begin{gathered} 20=a(60)^2 \\ (20)/(3600)=a \\ \\ a=(1)/(180) \end{gathered}`

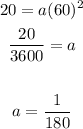
Now the equation of parbola is

`y=(x^2)/(180)`

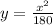
now the coordinate of focus is

`(h,k+(1)/(4a))`

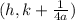
substitute all the values

`\begin{gathered} (0,0+(1)/((4)/(180))_) \\ \\ (0,45) \end{gathered}`

Final answer:

Coordinate of focus is