Given expression for function :

The general form of equation is :

The axis of symmetry is define as : the line that divides the parabola into two equal halves,
i,e
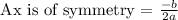
From the given expression we have a= 1, b =6, c=8
So,
Axis of symmtery = -6/2(1)
Axis of Symmetry = -3
i.e x = -3
Now for the vertex
Vertex : which is the minimum point of the parabola and the parabola opens upward.
for vertex
Substitute the x = -3 and solve for the valur of f(x)
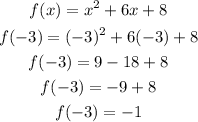
So the vertex will be (-3, -1)