Let x be number of widgets produced in 3 1/2 weeks.
The proportion therefore between the two ratios is
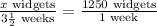
To solve for the number of widgets they can produce, multiply both sides by 3 1/2, to cancel out the denominator on the left side of the proportion.

Therefore, they can produce 4375 widgets in 3 1/2 weeks.