According to the given data we have the following expression:
7×8 4/5
In order to find out which shows how the distributive property can be used for we would have to make the following:
First convert mixed numbers to improper fraction
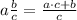
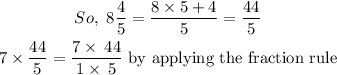
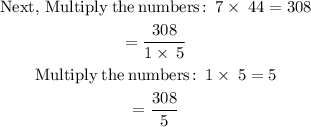
Finally, convert the improper fraction to mixed number:
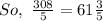
Therefore, the option that shows how the distributive property can be used to evaluate 7×8 4/5 would be the first option.