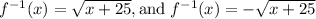Answer:
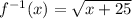 and
and

Explanation:
To find the inverse, we will set f(x) equal to y, swap the x and y values, and then solve for y.
Given:
f(x) = x² - 25
Equal to y:
y = x² - 25
Swamp x and y values:
x = y² - 25
Add 25 to both sides of the equation:
y² = x + 25
Square root both sides of the equation:
 and
and
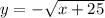
Interval notation: