We have a line that passes through point (0,3) and (-4,0).
Slope-intercept form:
We can calculate the slope of the line as:
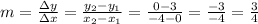
The y-intercept can now be calculated using the slope and one of the points:
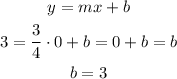
Then, we can express the equation as:

Direct variation:
We can not express as a direct variation line as the line do not go through the origin.
Point-slope form:
This form is:

We have to know the slope and one point in order to be able to write it.
The slope is 3/4 and one of the points is (0,3). We can write it as:

Two intercept form:
This form is:
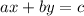
We can write this for our case as:
When x=0, y=c/b=3, and when y=0, x=c/a=-4.
We can write that c=1, and then b=1/3 and a=-1/4.
Then, our equation becomes:
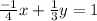
If we multiply both sides by 12 (the common factor of 3 and 4), we would get:
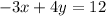
that is equivalent to the previous equation.