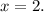Answer:
Computing the sum of fractions on the left side of the equation, we get:
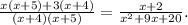
Now, notice that:
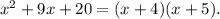
Therefore, we can rewrite the equation as:
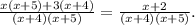
The above result implies that:
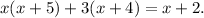
Simplifying the above equation, we get:
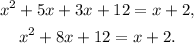
Subtracting x+2, we get:
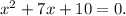
Notice that:
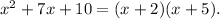
Therefore,
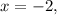
because x≠-5, otherwise we could not have a denominator of x+5.
Answer: