Question

The Freebody diagram represents a 1.5 kg box resting on an inclined plane what is the component of the weight parallel to the incline plane be what is the component of the web perpendicular to the inclined plane

Answer 1

part. 1: b. -7.35 N

part 2: -12.73 N

Step-by-step explanation:

The free-body diagram of the object is given below:

The green arrows above tell us the direction of the positive x - and y-axis in our twisted coordinated system.

Now, what is the magnitude of the weight parrallel to the incline (the blue line). It turns out that the answer is

`W_(\mleft\Vert \mright?)=-mg\sin 30^o`

Now in our case, m = 1.5 kg and g = 9.8 m/s^2; therefore. the above gives

`W_(\Vert)=-(1.5)(9.8)\sin 30^o`

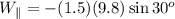
which evaluates to give

`\boxed{W_(\mleft\Vert \mright?)=-7.35N}`

This tells us that the weight of the box parallel to the incline is -7.35 N.

Now, what is the magnitude of the red arrow (the perpendicular component of weight) ? From trigonometry, we have

`W_(\perp)=mg\cos 30^o`

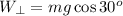
SInce in our case m = 1.5 and g = 9.8 m/s^2, we have

which evaluates to give

`W_(\perp)=-12.73N`

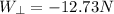
Hence, the perpendicular component of weight is -12.73 N.

Therefore, to summerise:

part. 1: b. -7.35 N

part 2: -12.73 N